Aceleradores divinos, ó E=MC²
Hablando en concreto sobre la exposición que os comento, son una serie de 56 fotografías de alta calidad, tomadas de diferentes partes del CERN, que aunque ya no está en Madrid según tengo entendido, seguirá aún en nuestro país, visitando Santiago de Compostela del 13 al 25 de noviembre, y Sevilla del 29 de noviembre al 11 de diciembre.

Exposición «El CERN a través de los ojos de Peter Ginter, la visión de un poeta»
Y volviendo al tema que nos ocupa, voy a intentar explicar a grandes líneas los principios de un acelerador de partículas. Para comenzar, debemos saber que hay varios tipos de aceleradores, pueden ser lineales (como el SLAC) o circulares, ciclotrones (un tipo de acelerador circular en forma de dos D’s enfrentadas, usados en aplicaciones de baja energía), etc. Nosotros nos centraremos en el funcionamiento de los aceleradores circulares, aunque la base es la misma para todos. El concepto que se encuentra detrás de los aceleradores, es el de campos magnéticos muy fuertes que van oscilando transmitiendo de esta forma energía a las partículas cargadas que se encuentran en su interior, las cuales comienzan a acelerarse hasta velocidades cercanas a la de la luz.
En ocasiones, se utiliza un acelerador lineal como «cañón» de partículas que luego pasan a un acelerador circular. Posteriormente, en este acelerador circular, las partículas continuan acelerándose con campos que se sincronizan con el movimiento de las mismas, para que su trayectoria mantenga un radio constante aunque su velocidad vaya en aumento. Pero hay un límite para dicha velocidad (como sabemos, en nuestro universo nada puede desplazarse más rápido que la luz en el vacío). Por lo que cuando se alcanza una velocidad en torno al 99’9% de la velocidad de la luz, el efecto que se consigue si continuamos transmitiendo energía a las partículas, es que su masa crece, las partículas se vuelven más pesadas (como sabemos, según la expresión de la teoría de la relatividad de Einstein, E=MC², por lo que si E aumenta y C permanece constante, M debe aumentar). Pensemos que un electrón con una energía de 1 MeV tiene una masa 3 veces mayor que un electrón en reposo, y que en el famoso LHC (del que hablaremos más adelante), se manejan protones con una energía de 7 TeV… ¡imaginemos cuánto debe aumentar su masa! Esto da paso a una de las utilidades más importantes de los aceleradores, que es el experimento de colisión de partículas. Para ello, se forman diferentes «rayos» de partículas que viajan en direcciones opuestas a velocidades cercanas a la de la luz, con una masa mucho mayor que cuando se encuentran en reposo. En determinados momentos, se hacen colisionar los rayos que viajan en direcciones opuestas, produciéndose colisiones entre partículas con una elevadísima energía.
Como adelantábamos, el LHC o Gran Colisionador de Hadrones, es un gigantesco acelerador circular (realmente formado por secciones rectas y curvas) y colisionador de partículas de reciente construcción (de una construcción que ha durado 15 años), situado en el CERN cerca de Ginebra, entre Francia y Suiza, en el que se hacen colisionar protones con una energía de 7 TeV cada uno, que viajan en direcciones opuestas a una velocidad muy cercana a la de la luz. La idea es que mediante estas colisiones, se puedan estudiar fenómenos parecidos a los que se produjeron en el Big Bang. En la actualidad, este LHC es el acelerador más grande del mundo, aunque su actividad ha sido realmente baja, ya que debido a una fuga de helio el 19 de septiembre de 2008, se ha cesado su funcionamiento hasta la reparación. Se espera que en este mes de noviembre se vuelva a poner en funcionamiento con energías de 3’5TeV, y que en 2010 alcance el punto de 7 TeV.

Interior del LHC
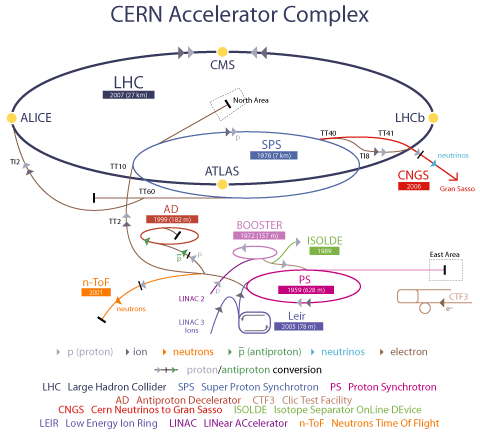
Esquema general LHC
Cabe mencionar que el LHC cuenta con unos 10.000 imanes, de los cuales 1.600 son superconductores. Los superconductores que podemos encontrar en el LHC utilizan cables de Niobio-Titanio. Para generar los campos magnéticos necesarios para transmitir 7 TeV a los protones, se deben hacer circular 11.700 amperios por los cables que acabamos de mencionar, por lo que es de vital importancia que no opongan resistencia a la electricidad, ya que de lo contrario se fundirían por el calor. Para que estos imanes superconductores puedan operar correctamente, deben encontrarse en un ambiente frío, y no nos referimos a frío como el que hace en Ávila una noche de invierno, sino a temperaturas cercanas al cero absoluto, para ser más exactos a -271’3ºC (aunque ya a -264ºC, los cables de Niobio-Titanio son superconductores). Esto se consigue con unas 120 toneladas de helio, y se tarda varias semanas en alcanzar esas condiciones. Podemos decir que LHC es uno de los lugares más fríos del planeta.
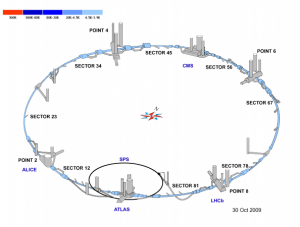
Situación térmica del LHC
A continuación, podéis ver un vídeo donde explican perfectamente el recorrido de las partículas desde que se introducen en el primer anillo hasta el momento de las colisiones… ¡os lo recomiendo! (está en inglés, eso sí).
Algunos de vosotros quizá os preguntéis… ¿qué tiene que ver este artículo con el título? ¿por qué hablan de cosas «divinas»? Pues bien, todo tiene su explicación.
Resulta que de las colisiones entre los protones en los aceleradores, se pueden obtener una serie de partículas subatómicas objeto de estudio. Una de estas partículas es el llamado Bosón de Higgs o la «Partícula de Dios«. Este nombre tan enigmático encierra tras de sí el último escalón para alcanzar la unificación del modelo estándar, que no alcanza a ser una teoría completa de las interacciones entre partículas fundamentales porque no incluye la gravedad.
El Bosón de Higgs es una de estas partículas fundamentales, por ahora hipotética, que según el modelo estándar debería existir, pero que aún no se ha encontrado experimentalmente. Esta partícula podría ser la responsable de la masa de otras partículas, y así, de muchas de las propiedades de la materia que conocemos.
Fruto de estos experimentos, han surgido multitud de corrientes más o menos fantasiosas, algunas con base «científica» y otras no tanto. Cabe mencionar a quienes piensan que cuando el LHC entre en funcionamiento a pleno rendimiento, podría provocar un agujero negro en nuestro proprio planeta. Pero una de las declaraciones que más me han llamado la atención al respecto del asunto, es la de los físicos Holger Bech Nielsen y Masao Ninomiya, que sostienen la posibilidad de que el propio Bosón de Higgs haya viajado en el tiempo para sabotear el funcionamiento del LHC, y de esta forma impedir o retrasar su propio descubrimiento.
“[..] el hipotético bosón de Higgs… podría ser una aberración tal para la naturaleza, que su creación podría producir de algún modo una ondulación a través del tiempo que detuviese el colisionador de hadrones antes de que el descubrimiento se produjese; igual que si un viajero en el tiempo viajase al pasado para matar a su abuelo e impedir así su viaje”.
Sin duda, teorías rocambolescas propias del mejor cine de ciencia ficción. Pero también es cierto que con estos experimentos, avances y descubrimientos científicos, cada vez la barrera entre la ciencia y la ficción resulta más difusa.
Podríamos seguir hablando páginas y páginas sobre este tema, sobre el Fermilab (otro acelerador, situado en Chicago) y de cómo intentan descubrir el Bosón de Higgs antes que el LHC aprovechando la avería de este último, sobre otros de los experimentos que se llevan a cabo en los aceleradores, sobre algunas curiosidades (como que en la red de ordenadores del LHC se utiliza una distribución de Linux llamada Scientific Linux, o que sus imanes pueden llegar a almacenar una energía de 10 gigajulios, o que la película Ángeles y Demonios trata sobre el tema de nuestro post, o que recae sobre Tom Hanks, protagonista de dicho film, la responsabilidad de «pulsar el botón» para volver a poner en marcha el LHC después de su avería en la vida real…), y siempre nos quedarían cosas que contar.

Vista aérea del LHC y el Fermilab
Para terminar, os dejo un link a otra web donde podréis encontrar más información sobre el LHC, y vídeos sobre su proceso de construcción emitidos en National Geographic: http://www.laparticuladedios.com/
Esperamos que este artículo os haya resultado entretenido, y ya sabéis, si os cruzáis con un protón al 99’99% de la velocidad de la luz… intentad esquivarlo. Esto me recuerda a algo que escuché cuando era pequeño…
«-¿Por qué la luz se propaga en el vacío a 300.000 km/s y en línea recta?
– Porque a esa velocidad es difícil coger las curvas.»
¡Hasta pronto!
Buenos días,
Os sigo desde hace tiempo y jamás he hecho una pregunta… pero es que tengo una duda muy grande con respecto al tema que tratais.
Es sobre el aumento de la masa cuando algo alcanza velocidades cercanas a la de la luz. Se dice que un protón puede alcanzar hasta siete mil veces su propia masa… ¿pero aumenta también de tamaño y/o densidad? ¿O es que existe algún tipo de diferencia entre la masa considerando «eso» que se opone al movimiento y la masa considerada como «eso» que origina la gravedad? Probablemente se trata de que mi pobre intelecto no alcanza según qué cosas, pero agradecería respuesta.
Un saludo.
Buenas tardes Jerbbil!
En primer lugar, queremos darte la bienvenida como usuario activo a nuestro blog, e invitarte a que nos hagas todas las preguntas que quieras, y que nosotros intentaremos responder dentro de nuestras posibilidades, así que.. ¡muchas gracias por participar!
Ahora, centrándonos en el tema que preguntas, he de decir que nuestro artículo no ha sido del todo correcto, sino que en él hacemos una aproximación, y es el hecho de que cuando aumentamos la energía de un objeto, a velocidades bajas casi toda esa energía se traduce en acelerar el objeto (y muy poca energía se invierte en aumentar su masa). Sin embargo, cuando el objeto se mueve a muy altas velocidades, casi toda la energía se emplea en aumentar la masa del objeto, ya que la velocidad de la luz es una constante que en la práctica no podremos alcanzar, y cuanto más nos acerquemos a ella, más proporción de la energía se traducirá en aumento de masa; la velocidad tenderá asintóticamente a C (velocidad de la luz en el vacío), pero (por ser asintóticamente) no llegará a tomar dicho valor.
En cuanto a lo que comentas sobre las diferencias entre un tipo de masa y otro, para precisar podemos contemplar los siguientes tipos de masa:
Masa invariante, también conocida como masa en reposo, que es una magnitud independiente del observador.
Masa relativista aparente, o simplemente masa aparente, que es una magnitud dependiente del sistema de referencia que incrementa su valor con la velocidad.
Masa inercial aparente, sería el cociente entre la fuerza aplicada a una partícula y el módulo de la aceleración observada.
Así, en el caso que tratamos en el post, nos estamos refiriendo a la masa relativista. Y para una partícula que no se mueva a la velocidad de la luz, la masa relativista será M=Ɣ · m, donde m es la masa en reposo del objeto, y Ɣ es el conocido como Factor de Lorentz, que toma diversos valores según la diferencia de velocidad entre el observador y el objeto en sí. Cuando ambos se desplazan con la misma velocidad, Ɣ valdrá 1, y M coincidirá con m.
De forma gráfica, puedes ver la variación de Ɣ en función de la velocidad, en la siguiente gráfica:
Como ves, las cosas se vuelven más enrevesadas cuantas más preguntas nos hacemos. De hecho, la famosa fórmula E = mc² es cierta para todos los observadores sólo si a m se la considera como masa relativista, ya que si la consideramos como masa invariante, la expresión sufre algunos cambios.
¡Esperamos que estas explicaciones te hayan servido para aclararte un poco más y no para liarte!
Un saludo.
Leonard.
Muy bueno el post, y saludos de Susy para Sheldon.
[…] Aceleradores divinos, ó E=MC² […]
Recordando la famosa paradoja de los gemelos, de Einstein, me pregunto si las interacciones entre los hadrones a la velocidad de la luz ocurrirán como en cámara lenta, y el producto de los choques tendrán una vida mucho mas larga que si ocurriera al 80% de c.
Muy buen post. Claro, escueto y entretenido.
Buscando cositas para el mío, he dado con este, y prometo repetir.
Por cierto, que no series «expertos en este tema», pero ya quisieran muchos expertos explicar las cosas con tanta claridad.
Hola abuela! 🙂 Por un momento pensé que era mi anciana abuela la que había dejado un comentario! 🙂
Queríamos darte la bienvenida a Átomos y Bits, y agradecerte que te hayas pasado por nuestras páginas! Los comentarios como el tuyo nos animan a seguir escribiendo, y nos hacen sentirnos acompañados en el ciberespacio 🙂 Y si encima te somos de utilidad para escribir tus posts, pues mejor que mejor!
Supongo que la velocidad a la que se produce el choque, dependerá del punto de vista del observador: si consigues surfear sobre una de las partículas que van a colisionar, vas a verlo muy diferente a como lo verán los científicos desde fuera! 🙂
Esperamos que te sigas pasando por nuestro blog, y que nos comentes todo lo que quieras! Hasta pronto.
Leonard.
[…] c es la velocidad mayor energía se necesita. En el gráfico energía/velocidad la velocidad de la luz marca asíntota a infinito. Vamos: intentemos mover toda la masa de un planetoide a velocidades relativistas y tendremos una […]
[…] del origen del universo. Sin embargo, todos los intentos de obtener monopolos magnéticos en los aceleradores de partículas han fracasado. Pero volvamos a los que sí existen, demostrados por la física, a los dipolos […]
[…] del origen del universo. Sin embargo, todos los intentos de obtener monopolos magnéticos en los aceleradores de partículas han fracasado. Pero volvamos a los que sí existen, demostrados por la física, a los dipolos […]