La frecuencia, esa gran desconocida.
¡Hola de nuevo, queridos lectores!
Volvemos una vez más con un tema que tratamos a diario sin que muchos de nosotros lleguemos a darnos siquiera cuenta de ello. Se trata de la frecuencia, presente en prácticamente todos los aspectos de nuestra vida cotidiana, pero invisible para nuestra mente habituada a trabajar en el dominio del tiempo.
En realidad, la frecuencia en sí misma es un tema tan inmensamente amplio, que no podríamos cubrirlo entero ni en un año de posts, así que esto será simplemente una serie de pinceladas, que ayudarán a los menos iniciados en el tema a comprender un poco mejor este concepto.
La frecuencia es una magnitud que mide el número de repeticiones de un determinado fenómeno o suceso periódico. Con esta descripción tan amplia, no es de extrañar que tenga aplicaciones en numerosísimos campos de nuestra vida. Su unidad es el hercio, en honor a Heinrich Rudolf Hertz . Un hercio no es más que una repetición de un evento periódico en un segundo. Dicho de otra forma, 1 Hz = 1/s. Por tanto sus unidades nos indican una relación inversa al tiempo.
Podemos encontrar frecuencia en cualquier evento que se repita. Por ejemplo, el número de ciclos por segundo con que es capaz de operar el microprocesador de un ordenador, o el reloj de nuestra tarjeta gráfica, o las vibraciones que producen un determinado sonido, o las ondas implicadas en una comunicación entre un emisor de radio y nuestra radio de toda la vida… Si consiguierais leer 5 artículos de Átomos y Bits por segundo, estaríais leyendo artículos con una frecuencia de 5 hercios. Como veis, muchas cosas son susceptibles de explicarse en términos de frecuencia. El espectro de frecuencias está dividido en una serie de bandas, cada una de las cuales presenta unas determinadas características a la hora de ser utilizadas para telecomunicaciones.
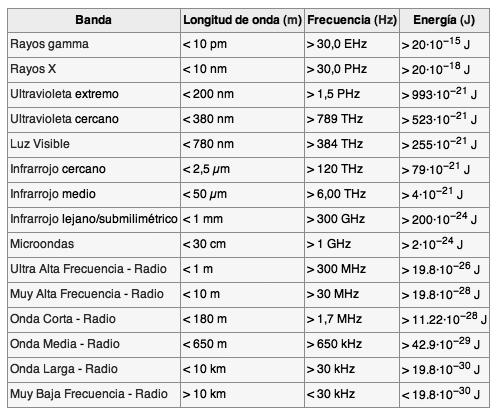
Bandas de frecuencia. Fuente: Wikipedia
Hay varios conceptos importantes relacionados directamente con la frecuencia. Uno de ellos muy utilizado en todo lo relacionado con señales, es el período de una señal. El período (normalmente expresado como «T») no es más que el tiempo que transcurre entre una repetición del evento y la siguiente. Se calcula como el inverso de la frecuencia (T=1/f). Las señales de variación más lenta tendrán un período mayor que las de variación más rápida, o sea, a mayor frecuencia menor período, y viceversa.
Otra idea que es básica en todo lo relacionado con la frecuencia, es la longitud de onda, magnitud inversamente proporcional a la frecuencia, en al que interviene también la velocidad de la propia onda (habitualmente suele aproximarse por la velocidad de la luz en el vacío), según la siguiente igualdad:
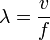
Esta magnitud nos dice cuánto espacio mide un período de la señal, una repetición. Dicho de otra forma, nos dice el espacio que hay entre dos puntos en los que, al pasar la onda por ellos, produciría una amplitud similar (en módulo y fase) del campo electromagnético. Para que nos hagamos una idea, una onda de 2 mHz (milihercios) tiene una longitud de onda aproximadamente igual a la distancia entre la Tierra y el Sol. Esto tiene sus implicaciones: en telecomunicaciones existen ciertas limitaciones a la hora de transmitir en onda larga, y es que las antenas deben guardar una cierta proporción con respecto a la longitud de onda en que se está trabajando. A menudo, suelen medir λ/4 (aunque la Torre de Radio de Varsovia tenía una longitud de λ/2), pero por efecto espejo con la tierra, equivale a tener una antena de altura λ/4 hacia el cielo, y otra simétrica de «profundidad» λ/4 hacia el suelo, por tanto es una longitud total de λ/2. Evidentemente, si se desea trabajar en esa banda de frecuencias tan bajas, existen ciertos límites ya que no podemos construir antenas de una altura exagerada por todos los problemas que dicha construcción implicaría.

Antena Marconi típica de onda corta. Fuente: http://freeradionova.com/
Bien, llegados a este punto ya tenemos una idea un poco más clara de en qué consiste la frecuencia. Pero, ¿por qué se utiliza tanto cuando hay que trabajar con ondas? ¿No sería más sencillo expresarlo todo en función del tiempo? Puede parecer que sí, pero en realidad trabajar con frecuencias tiene sus ventajas. Para empezar, poder «mover» las señales de una frecuencia a otra, montando una señal de una cierta frecuencia en otra de una frecuencia superior, es una de las claves del progreso tecnológico que experimentamos hoy en día. Consiste en que una onda (la portadora) varíe alguno de sus parámetros (su amplitud, su frecuencia…) en función de las variaciones de otra onda (la moduladora), que es la información que queremos transmitir. Seguramente conoceréis este uso de la frecuencia con el nombre de modulación. Esta técnica permite aprovechar mucho mejor el canal de comunicaciones, hacerlo más resistente frente al ruido, y poder enviar más información simultáneamente a través del mismo canal. Existen un gran número de tipos de modulaciones posibles: AM (modulación en amplitud), FM (modulación en frecuencia), PM (modulación en fase), DSB (en doble banda lateral), QAM (amplitud en cuadratura), etc., cada una con sus ventajas y sus inconvenientes.
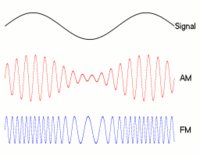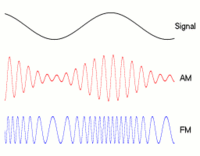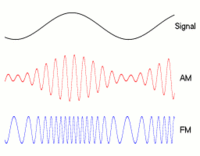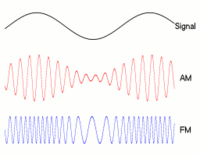
Onda de baja frecuencia (portadora, las dos de abajo) puede modularse en amplitud (AM, varía la amplitud) o en frecuencia (FM, varía la frecuencia). (Fuente: Wikipedia)
Vale, ya hemos visto que podemos expresar la información de las ondas en función de la frecuencia (teóricamente, cualquier onda por extraña que sea puede ser expresada como una suma de infinitas ondas a diferentes frecuencias), pero ¿cómo se realiza este paso de ondas en el dominio del tiempo a ondas en el dominio de la frecuencia? Gracias a una herramienta muy útil: la Transformada de Fourier, que puede ser expresada de forma general mediante la siguiente ecuación:
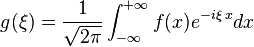
Trabajando con transformadas, podemos operar con relativa facilidad dos señales, además de poder observar sus características espectrales con mucha comodidad (por ejemplo para ver en qué parte del espectro de frecuencias se concentra la mayor parte de su potencia). Por ejemplo, si trabajamos con la clásica señal «seno» o «coseno», sus transformadas de Fourier no son más que dos picos (o deltas) de energía, uno en la frecuencia +w y otro en la frecuencia simétrica -w. Son muy numerosas las características propias de las operaciones con señales y con sus transformadas que hacen interesante el uso de esta herramienta (por ejemplo, las transformadas de la multiplicación de dos señales, o de la convolución de dos señales), pero su estudio se escapa del alcance de este post, aunque os invitamos a que les echéis un vistazo si el tema os resulta interesante.
Para terminar, os comentaré que trabajar con cada rango del espectro tiene sus ventajas e inconvenientes, y por ello las comunicaciones se dan en unas u otras frecuencias dependiendo de los requisitos que se quieran cumplir. Así, por ejemplo, trabajar en Onda Corta nos permite cubrir largas distancias, ya que la onda rebota a diferentes alturas (a mayor frecuencia mayor altura), pudiendo hacerlo incluso en la ionosfera, y llegando así a puntos con los que el emisor no tiene línea de visión directa. Dentro de esta banda, hay sub-bandas más adecuadas para transmitir de noche o transmitir de día. Si se trabaja a mayores frecuencias, la absorción causada por obstáculos, nubes, etc., tiene mayor efeto en la comunicación, con lo que las pérdidas aumentan. Cada rango de frecuencias presenta unas determinadas características de atenuación intrínseca y de pérdidas, que determinan el uso que se puede hacer de ellas.
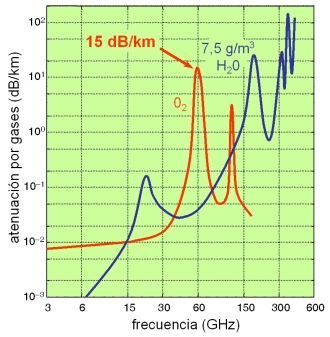
Los gases y vapores atmosféricos también introducen atenuación en los radioenlaces de alta frecuencia. Fuente: www.radioptica.com
En fin, queridos lectores, con este tema abrimos todo un abanico de otros posibles temas a tratar, como son los radioenlaces, las interferencias, las comunicaciones por satélite, las comunicaciones móviles, etc. Esperamos que os haya resultado interesante, y que si bien es sólo introductorio, os permita tener una idea mejor de qué se esconde detrás de una palabra tan frecuente como frecuencia. ¡Hasta pronto!


Hola Leo!!
Enhorabuena por el artículo! A mí me ha parecido muy interesante! La verdad, ahora tengo más imagen de qué es frecuencia 🙂
Gracias, no dejéis de escribirnos!!
Besitos,
Sasha
Muchas gracias Sasha 🙂
Seguiremos escribiendo mientras que haya gente como tú que nos siga leyendo.
Hasta pronto.
[…] La frecuencia, esa gran desconocida. […]
Amigo, muchisimas gracias, este articulo a sido de gran ayuda para mi tecnologia. . .
De nuevo mil gracias. . .
Me alegro mucho de que te haya sido útil el artículo!!
Muchas gracias a ti por leernos 🙂
Saludos! Hasta pronto.
saludos, buen contenido, estoy repasando algunos conceptos para hacer algo alrespecto de ruido «es como la religion para muchos» habria que conseguir antiondas o materiales opacos al ruido (para mi: reggeton, salsa, graves, ruido blanco, bandas) ideal seria un material filtro que solo dejara pasar sonidos a elecccion (bossanova original, sonidos de la naturaleza) haber que surge.
[…] nos indican la capacidad de procesamiento de nuestros microprocesadores o, dicho de otra manera, la frecuencia de su reloj. Mi ordenador actual es de 3,5 Ghz, que son 3,5×109 o unos 3.500.000.000 ciclos por […]