El Principio de Arquímedes y el final de los orfebres malvados
“Un cuerpo total o parcialmente sumergido en un fluido estático, será empujado con una fuerza vertical ascendente igual al peso del volumen de fluido desplazado por dicho cuerpo”

Arquímedes por José Ribera. Museo del Prado.
Bienvenidos de nuevo queridos lectores, hoy me gustaría hablaros acerca de uno de los más grandes genios de la historia del hombre, Arquímedes, y su famoso Principio. Imagino que todos conocemos la famosa historia en la que Hierón II pidió a Arquímedes (del cual, por cierto, era primo carnal) que verificase la autenticidad de su nueva corona de oro. Hierón II había entregado un lingote de oro puro a un orfebre y desconfiaba de si éste se había quedado parte del oro sustituyéndolo por plata o cobre.
Arquímedes no tenía del todo claro cómo demostrarlo y se pasaba el tiempo dándole vueltas al problema, pues, obviamente no podía fundir la corona para medir su densidad. Por aquel entonces Arquímedes ya intuía parte del que sería el principio de la hidrostática, pues había notado como el agua aumentaba de nivel al sumergir algo en ella y que, dentro del agua podía mover las piernas con más facilidad porque parecían “pesar” menos.
Dado que el agua es incompresible (es decir, no varía su densidad), al sumergir un cuerpo en ella, ésta debería desplazarse. ¿Cuánto? Pues fácil, la misma cantidad de volumen que se había sumergido en ella. ¿Por qué? Bueno, es lógico pensar que si en una bolsa de canicas meto, por ejemplo…ehh… un cubo de rubik! El volumen total de la bolsa será el de las canicas más el del cubo de rubik, ¿verdad? A menos que pudiese disminuir la distancia entre las canicas. Cómo el agua es incompresible y eso significa que no puede variar su densidad (la distancia entre las canicas) deducimos que el volumen desplazado, forzosamente, es el mismo que el del cuerpo sumergido.
Y aquí es donde nos cuentan cómo, mientras se daba un baño, llegó a su mente la solución al problema y salió corriendo por las calles de Siracusa desnudo gritando ¡Eureka! ¡Eureka!, que significa ¡Lo encontré! ¡Lo encontré! Pues bien, esta anécdota, según me enteré hace poco, es falsa.

¡Eureka! ¡Lo encontré!
De pequeño también nos contaron, o al menos a mí, que tomó la corona de Hierón II y una cantidad de oro (Arquímedes era rico, por si no lo sabíais) igual a la utilizada para su fabricación. Preparó, además, unos recipientes iguales llenos de agua y sumergió la corona en uno y el oro en el otro. Según su propio Principio (el de Arquímedes, ¡claro!) el volumen de agua desalojado debería ser el mismo en ambos casos si la corona fuera de oro macizo. Sin embargo, parece que esta historia tampoco es todo lo fidedigna que debería, entre otras cosas porque si el método seguido por Arquímedes fuese exactamente el descrito apenas habría podido distinguir diferencias en los desplazamientos de agua. Enseguida veremos por qué. Para ello deberemos hacer algunos cálculos, todos ellos sencillos, así que no os asustéis.
Como ya hemos comentado, Arquímedes ya conocía el desplazamiento del agua y esa especie de flotación que parecían sufrir los cuerpos una vez sumergidos. Pero además, también se había fijado en que el cociente entre el peso de un cuerpo y su volumen (es decir, su densidad) parecía ser una propiedad intrínseca del propio material. Estableció la densidad del agua en 1 g/cm3, la del oro en 19,3 g/cm3 y la de la plata en 10,6 g/cm3.
Con estos valores podemos calcular el volumen de la corona. La corona más grande que se ha encontrado de los tiempos de Arquímedes pesa 714 gramos. Como puede que con el tiempo se hayan perdido alguna de sus partes vamos a aproximar su peso a 800 gramos. Por lo tanto, si la corona fuera de oro macizo tendría un volumen de 800 g / 19,3 g/cm3 = 41,450 cm3.
Si suponemos que el orfebre había cambiado un 30% del oro por plata, eso significa que la corona tendría 560 gramos de oro y 240 de plata. El volumen de la parte de oro sería de 560 g / 19,3 g/cm3 = 29,016 cm3 y el de la parte de plata de 240 g / 10,6 g/cm3 = 22,642 cm3 lo que haría en total una corona de 51,658 cm3.
Pues bien, ahora suponemos que para medir el desplazamiento del agua se utilizó un recipiente circular de unos 25 cm de diámetro. Esto nos da una base de (πr2) 491 cm2. Podemos calcular cuánto sube el nivel del agua en cada caso simplemente dividiendo el volumen de cada corona por la superficie de la base del recipiente. ¿Por qué así? Pues porque al introducir la corona desplazamos una cantidad de agua igual al volumen de la corona y esa cantidad de agua debe repartirse a lo largo de la superficie del recipiente.
Por lo tanto, en el primer caso, con la corona de oro macizo, el agua debería haberse desplazado 41,450 cm3 / 491 cm2 = 0,084 cm. Mientras que en el segundo caso, con la corona mezclada al 30% con plata, el agua debería haberse desplazado 51,658 cm3 / 491 cm2 = 0,105 cm. Esto supone una diferencia entre ambos casos de 0,105 – 0,084 = 0,021 cm, o, lo que es lo mismo, ¡0,21 mm! No había manera de que Arquímedes pudiese medir tal diferencia en aquella época, por lo tanto ese no pudo ser el método seguido para demostrarlo.
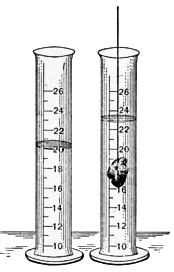
Desplazamiento de fluido
Pero si eso utiliza el Principio de Arquímedes y aun así Arquímedes no pudo hacerlo de esa manera ¿cómo lo hizo? Pues bien, lo que hizo Arquímedes fue utilizar la parte de su Principio que dice que, además de desplazar el fluido, se genera un empuje vertical igual al volumen del cuerpo sumergido.
Esto significa que nuestra corona de oro macizo en el agua pesa sus 800 gramos menos los 41,450 gramos de agua que desplaza (ya que el agua tiene una densidad de 1 g/cm3), es decir, tiene un peso aparente de 758,55 gramos. Por otra parte, la corona falsa pesaría 560 g – 29,016 g más 240 g – 22,642 g , es decir, 748,342 gramos. Así, dado que la diferencia en peso entre las coronas es de 10,208 gramos y en aquella época si era medible tal diferencia, lo único que le quedaba por hacer a Arquímedes era introducir una balanza dentro del agua y medir la diferencia de peso entre la corona de Hierón II y su equivalente peso en oro. Si la corona hubiese sido falsa la balanza se habría inclinado hacia el lado del oro, pues la diferencia en volumen habría generado un empuje vertical mayor sobre la corona falsa que sobre la verdadera.
¿Cuál fue la conclusión en cuanto a la corona? ¿Era verdadera? ¿Era falsa? Pues la verdad es, amigos lectores, que no lo sé. He encontrado multitud de fuentes donde se dice que la corona era falsa, pero también he encontrado alguna otra fuente de peso que, mediante el método expuesto, afirma que Arquímedes demostró que la corona estaba fabricada en oro macizo. Así que lo dejo a vuestra elección. Ahora que sabéis cómo lo hizo el siracusano, podéis recrear la historia en casa a vuestro antojo.


Muy buena esta lección de historia la cual por supuesto desconocía.
De todas formas me surge una duda, no habría bastado con poner una bascula (fuera del agua) y poner por un lado la corona y por el otro el lingote? Por mucho que hubiera el orfebre intentado igualar el peso del lingote, solo si hubiera usado todo el oro pesarían lo mismo ¿no?
Muy buenas Javi,
el problema no es que no hubiera usado todo el oro, sino que la parte que se hubiese quedado la hubiese sustituido por plata de manera que el peso total de la corona fuese el mismo que el del oro que le dió Hierón II. En ese caso una balanza (ojo, que no es lo mismo que una báscula) fuera del agua habría permanecido en equilibrio. Arquímedes encontró la forma de traducir la diferencia de volumen (debido a la diferencia de densidades a pesar de la igualdad en peso) a empuje vertical para inclinar la balanza dentro del agua.
Un saludo!
Coño, pues si lo de la bañera era mentira este hombre es doblemente genio: Inventó el Marketing
yo no lo entendia y aora lo entiendo
muy bueno
muy buenos buenos días , no entiendo total que queria encontrar arquimedes , el volumen de lA CORONA , SU DENSIDAD O QUE ?… ESPERO SU RESPUESTA ..POR FAVOR ..GRACIAS
David,
lo que quería Arquímedes era únicamente determinar si la corona estaba completamente fabricada en oro o no, para saber si el orfebre que la había fabricado se había quedado con parte del oro que le había dado el rey. En realidad no «quería» calcular el volumen de la corona ni su densidad, pero se valió de ambos para determinar su veracidad o falsedad.
Un saludo.
Excelente historia…. es maravilloso tener una vision mas alla de lo que nos enseñan en la escuela
Rafael, muchas gracias por tan amables palabras. Esperamos poder ofreceros siempre contenidos de vuestro interés.
Un saludo.
[…] a la mítica frase atribuida al matemático griego Arquímedes, del que ya hemos hablado en otra ocasión. En realidad me refiero a la serie de Syfy (personalmente prefería Sci-Fi) con el mismo […]
Es un buen artículo con muy buena información.
Gracias me ha servido de mucho esta página web
Recomendare la página a todo el mundo que tenga que hacer un trabajo sobre el principio de arquimedes
Muchas gracias @mario! Estamos encantados de haberte sido de ayuda. No dejes de volver a visitarnos.
Un saludo.
[…] a la mítica frase atribuida al matemático griego Arquímedes, del que ya hemos hablado en otra ocasión. En realidad me refiero a la serie de Syfy (personalmente prefería Sci-Fi) con el mismo […]